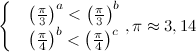Уровень: Выпускник (11 класс)
Условие. Пусть вещественные числа а, b, с удовлетворяют системе неравенств:
Тогда НЕВОЗМОЖНЫМ является выполнение неравенства:
Варианты ответа: А: a<c<b,Б: c<a<b, В: a=c<b, Г: a<b<c, Д: -b<-c<-a
Решение Основание первого показательного неравенства больше единицы, значит, a<b. Во тором же основание меньше единицы и соотношение между показателями будет: c<b. Выходит, b - самое большое из чисел. Так что неравенство a<b<c выполняться не может.
Ответ: Г: a<b<c.
Условие. Пусть вещественные числа а, b, с удовлетворяют системе неравенств:
Варианты ответа: А: a<c<b,
Решение Основание первого показательного неравенства больше единицы, значит, a<b. Во тором же основание меньше единицы и соотношение между показателями будет: c<b. Выходит, b - самое большое из чисел. Так что неравенство a<b<c выполняться не может.
Ответ: Г: a<b<c.
