Уровень: Малыш 3-4 (3 и 4 класс)
Условие. Кораблем можно перевезти за один раз или только 10 легковых автомобилей, или только 6 грузовиков. В среду корабль пересек реку пять раз и перевез 42 транспортных средства, будучи всегда полностью загруженным. Сколько легковых автомобилей перевез корабль в среду?
Варианты ответа: А:10, Б:12, В:20, Г:22, Д:30
Решение
Будем решать задачу по вопросам.
1. Сколько грузовиков можно перевести за 5 рейсов?
6х5=30
2. На сколько больше тридцати было перевезено машин в среду?
42-30=12
3.На сколько больше переводится за один рейс легковых машин, чем грузовиков?
10-6=4
4.Сколько было рейсов с легковыми машинами?
12:4=3
5. Сколько было перевезено легковых машин?
3х10=30
Ответ: Д:30.
Всё, что касается подготовки, проведения и результатов олимпиады.
воскресенье, 26 декабря 2010 г.
пятница, 10 декабря 2010 г.
Открыт блог по олимпиаде Кенгуру-2011
По адресу http://kenguru2011.blogspot.com/ открыт блог, посвящённый вопросам проведения Международной математической олимпиады Кенгуру-2011.
Согласно правилам проведения олимпиады, конкурс Кенгуру-2011 в Украине будет состоится в четверг, 17 марта 2011 года. Для участия в нём необходимо зарегистрироваться не позднее субботы, 12 февраля 2011.
Сумма благотворительного пожертвования участника не изменилась и составляет 10 гривен. Эти средства полностью используются для покрытия расходов на организацию и проведение конкурса.
Согласно правилам проведения олимпиады, конкурс Кенгуру-2011 в Украине будет состоится в четверг, 17 марта 2011 года. Для участия в нём необходимо зарегистрироваться не позднее субботы, 12 февраля 2011.
Сумма благотворительного пожертвования участника не изменилась и составляет 10 гривен. Эти средства полностью используются для покрытия расходов на организацию и проведение конкурса.
воскресенье, 28 ноября 2010 г.
Решение задачи про число 777 (Ш13)
Уровень: Школьник (5 и 6 класс)
Условие. На уроке математики Тарас записал некоторое число. Затем он разделил его на 7 и прибавил 7, а полученный результат умножил на 7. В результате получил 777. Какое число Тарас записал в самом начале?
Варианты ответа: А:7, Б:111, В:567, Г:722, Д:728
Решение
Решаем задачу с конца. Перед умножением было число 777/7=111, перед прибавлением семёрки - число 111-7=104 и перед делением на 7: 104/7=728 Ответ: Д:728
Условие. На уроке математики Тарас записал некоторое число. Затем он разделил его на 7 и прибавил 7, а полученный результат умножил на 7. В результате получил 777. Какое число Тарас записал в самом начале?
Варианты ответа: А:7, Б:111, В:567, Г:722, Д:728
Решение
Решаем задачу с конца. Перед умножением было число 777/7=111, перед прибавлением семёрки - число 111-7=104 и перед делением на 7: 104/7=728 Ответ: Д:728
вторник, 16 ноября 2010 г.
Решение задачи про сумму квадратов (В3) математической олимпиады Кенгуру 2010
Уровень: Выпускник (11 класс)
Условие. Сколько существует пар (х,у) чисел, удовлетворяющих уравнению (х-3)2 + (у-2)2=0?
Варианты ответа: А:1, Б:2, В:6, Г:32, Д:таких пар нет
Решение
Сумма двух квадратов равна нулю тогда, и только тогда, когда каждый из квадратов равен нулю. Таким образом x=3, y=2 - единственное решение.
Ответ: А:1
Условие. Сколько существует пар (х,у) чисел, удовлетворяющих уравнению (х-3)2 + (у-2)2=0?
Варианты ответа: А:1, Б:2, В:6, Г:32, Д:таких пар нет
Решение
Сумма двух квадратов равна нулю тогда, и только тогда, когда каждый из квадратов равен нулю. Таким образом x=3, y=2 - единственное решение.
Ответ: А:1
суббота, 6 ноября 2010 г.
Решение задачи про наибольшее число (К18)
Уровень: Кадет (7 и 8 класс)
Условие. Если, а - 1 = b + 2 = c - 3 = d + 4 = е - 5 то наибольшим среди чисел а, b, с, d, e есть число
Варианты ответа:
А:a, Б:b, В:c, Г:d, Д:e,
РешениеЧем число большое, тем больше от него нужно отнять, чтобы сравнять с остальными. Так что наибольшим является e
Ответ: Д:e
Условие. Если, а - 1 = b + 2 = c - 3 = d + 4 = е - 5 то наибольшим среди чисел а, b, с, d, e есть число
Варианты ответа:
А:a, Б:b, В:c, Г:d, Д:e,
РешениеЧем число большое, тем больше от него нужно отнять, чтобы сравнять с остальными. Так что наибольшим является e
Ответ: Д:e
воскресенье, 31 октября 2010 г.
Решение задачи про дни рождения
Уровень: Кадет, Малыш 3-4 (3, 4, 7 и 8 классы),
Условие. Виталик сложил числа дней и числа месяцев дат рождения всех своих друзей и получил 35. Даты рождения его друзей различны. Какое наибольшее возможное количество друзей у Виталика?
Варианты ответа: А:7, Б:8, В:9, Г:10, Д:12,
Решение Понятно, что наибольшее число друзей будет, если суммы чисел в их датах рождения минимальны. Сумма 2 будет у родившегося 1 января, Сумма 3 - у родившихся 1 февраля и 2 января, сумма 4 - у 3 января, 2 февраля и 1 марта. Для этих 6 человек сумма чисел дней и месяцев рождения составит 2+3+3+4+4+4=20. Добавим ещё трёх человек с суммой 5: 4 января, 3 февраля и 2 марта. Итого 9 друзей.
Ответ: В:9
Условие. Виталик сложил числа дней и числа месяцев дат рождения всех своих друзей и получил 35. Даты рождения его друзей различны. Какое наибольшее возможное количество друзей у Виталика?
Варианты ответа: А:7, Б:8, В:9, Г:10, Д:12,
Решение Понятно, что наибольшее число друзей будет, если суммы чисел в их датах рождения минимальны. Сумма 2 будет у родившегося 1 января, Сумма 3 - у родившихся 1 февраля и 2 января, сумма 4 - у 3 января, 2 февраля и 1 марта. Для этих 6 человек сумма чисел дней и месяцев рождения составит 2+3+3+4+4+4=20. Добавим ещё трёх человек с суммой 5: 4 января, 3 февраля и 2 марта. Итого 9 друзей.
Ответ: В:9
пятница, 22 октября 2010 г.
Решение задачи про степени (Ю23)
Уровень: Юниор (9 и 10 класс)
Условие. Для скольких натуральных чисел n от 1 до 100 включительно число nn является квадратом натурального числа?
Варианты ответа: А:5, Б:15, В:50, Г:54, Д:55,
Решение Во-первых, квадратом nn будет для чётного n. Таких чисел от 1 до 100 будет 50. Во-вторых, для нечётного n, являющегося квадратом. Таких n будет 5: 1, 9, 25, 49, 81. Итого 55 вариантов.
Ответ: Д:55
Аналогичная, но более сложная задача сейчас сдерживает наступление на Хребет натуральных чисел в игре Математические маневры.
Условие. Для скольких натуральных чисел n от 1 до 100 включительно число nn является квадратом натурального числа?
Варианты ответа: А:5, Б:15, В:50, Г:54, Д:55,
Решение Во-первых, квадратом nn будет для чётного n. Таких чисел от 1 до 100 будет 50. Во-вторых, для нечётного n, являющегося квадратом. Таких n будет 5: 1, 9, 25, 49, 81. Итого 55 вариантов.
Ответ: Д:55
Аналогичная, но более сложная задача сейчас сдерживает наступление на Хребет натуральных чисел в игре Математические маневры.
понедельник, 18 октября 2010 г.
Решение задачи про квадрат (Ш19) олимпиады Кенгуру 2010
Уровень: Школьник (5 и 6 класс)
Условие.
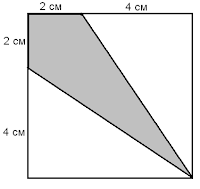
Вычислите площадь затемненной части квадрата
Варианты ответа: А:8 см2, Б:12 см2, В:18 см2, Г:24 см2, Д:36 см2
Решение
Разобьём этот квадрат диагональю, являющейся осью симметрии затемнённой фигуры. Тогда фигура разобьётся на два треугольника с основаниями 2 см, и высотами 6 см. Площадь одного такого треугольника равна 6 см2, а всей фигуры 12 см2
Ответ: Б:12 см2.
Условие.
Вычислите площадь затемненной части квадрата
Варианты ответа: А:8 см2, Б:12 см2, В:18 см2, Г:24 см2, Д:36 см2
Решение
Разобьём этот квадрат диагональю, являющейся осью симметрии затемнённой фигуры. Тогда фигура разобьётся на два треугольника с основаниями 2 см, и высотами 6 см. Площадь одного такого треугольника равна 6 см2, а всей фигуры 12 см2
Ответ: Б:12 см2.
понедельник, 4 октября 2010 г.
Решение задачи про последовательность (Ю25)
Уровень: Юниор (9 и 10 класс)
Условие. Первый, второй и третий члены последовательности равны соответственно 1, 2 и 3. Каждый последующий член последовательности, начиная с четвертого,
определяется по формуле аn = an-3 + аn-2 - аn-1, n Є N , n > 3 . Тогда а2010 =
Варианты ответа:
А:-2010, Б:-2006, В:2002, Г:2009, Д:2010,
Решение
Получим несоклько членов этой последовательности:
1, 2, 3, 0, 5, -2, 7, -4, 9, -6, …
Замечаем, что последовталеьность распадается на две. Её члены с нечётными номерами равны своему номеру, а с чётными a2n=4-2n.
Докажем это по индукции. Пyсть для всех n, меньших k a2n=2-2n и a2n+1=2n+1.
Тогда a2k+2 = a2k-1 + a2k - a2k+1 = 2k-1 + 4-2k – (2k+1) = 4-(2k+2)
a2k+3 = a2k + a2k+1 - a2k+2 = 4-2k + 2k+1 – (4-(2k+2)) = 2k+3
Значит a2010 = 4-2010 = -2006
Ответ:Б:-2006
Условие. Первый, второй и третий члены последовательности равны соответственно 1, 2 и 3. Каждый последующий член последовательности, начиная с четвертого,
определяется по формуле аn = an-3 + аn-2 - аn-1, n Є N , n > 3 . Тогда а2010 =
Варианты ответа:
А:-2010, Б:-2006, В:2002, Г:2009, Д:2010,
Решение
Получим несоклько членов этой последовательности:
1, 2, 3, 0, 5, -2, 7, -4, 9, -6, …
Замечаем, что последовталеьность распадается на две. Её члены с нечётными номерами равны своему номеру, а с чётными a2n=4-2n.
Докажем это по индукции. Пyсть для всех n, меньших k a2n=2-2n и a2n+1=2n+1.
Тогда a2k+2 = a2k-1 + a2k - a2k+1 = 2k-1 + 4-2k – (2k+1) = 4-(2k+2)
a2k+3 = a2k + a2k+1 - a2k+2 = 4-2k + 2k+1 – (4-(2k+2)) = 2k+3
Значит a2010 = 4-2010 = -2006
Ответ:Б:-2006
среда, 29 сентября 2010 г.
Решение задачи про лжецов (К26) олимпиады Кенгуру 2010
Уровень: Кадет (7 и 8 класс)
Условие. В городе Буле некоторые жители - лжецы, и они всегда врут, а все остальные всегда говорят правду. Однажды в одной комнате находилось несколько жителей этого города, и трое из них сказали следующее:
1) Нас здесь не более трех человек. Все мы - лжецы.
2) Нас здесь не более четырех человек. Не все мы лжецы.
3) Нас тут пятеро. Трое из нас лжецы.
Определите, сколько в комнате людей и сколько среди них лжецов.
Варианты ответа:
А: 3 человека, 1 лжец, Б: 4 человека, 1 лжец, В: 4 человека, 2 лжеца, Г: 5 человек, 2 лжеца, Д: 5 человек, 3 лжеца,
Решение Допустим, в комнате трое. Тогда первая фраза первого человека "Нас здесь не более трех человек" - истинна. Тогда должна быть истинной и вторая его фраза "Все мы - лжецы". Но она истинной быть не может. Значит, человек в комнате больше трёх.
Допустим, в комнате четверо. Тогда первый человек сказал неправду. Второй, соответственно, правду. А третий солгал. Значит, два лжеца уже есть (это первый и третий). А троих лжецов быть не может, поскольку третий солгал, сказав "Трое из нас лжецы". Так что ответ "4 человека, 2 лжеца" непротиворечив.
Ответ найден, но для интереса проверим, могло ли в комнате быть пятеро. В таком случае первые двое соврали. Значит, ложны их фразы "Все мы - лжецы" и "Не все мы лжецы". А т.к. это взаимоисключающие фразы, ложной из них должна быть только одна. Противоречие.
Ответ: В: 4 человека, 2 лжеца
Условие. В городе Буле некоторые жители - лжецы, и они всегда врут, а все остальные всегда говорят правду. Однажды в одной комнате находилось несколько жителей этого города, и трое из них сказали следующее:
1) Нас здесь не более трех человек. Все мы - лжецы.
2) Нас здесь не более четырех человек. Не все мы лжецы.
3) Нас тут пятеро. Трое из нас лжецы.
Определите, сколько в комнате людей и сколько среди них лжецов.
Варианты ответа:
А: 3 человека, 1 лжец, Б: 4 человека, 1 лжец, В: 4 человека, 2 лжеца, Г: 5 человек, 2 лжеца, Д: 5 человек, 3 лжеца,
Решение Допустим, в комнате трое. Тогда первая фраза первого человека "Нас здесь не более трех человек" - истинна. Тогда должна быть истинной и вторая его фраза "Все мы - лжецы". Но она истинной быть не может. Значит, человек в комнате больше трёх.
Допустим, в комнате четверо. Тогда первый человек сказал неправду. Второй, соответственно, правду. А третий солгал. Значит, два лжеца уже есть (это первый и третий). А троих лжецов быть не может, поскольку третий солгал, сказав "Трое из нас лжецы". Так что ответ "4 человека, 2 лжеца" непротиворечив.
Ответ найден, но для интереса проверим, могло ли в комнате быть пятеро. В таком случае первые двое соврали. Значит, ложны их фразы "Все мы - лжецы" и "Не все мы лжецы". А т.к. это взаимоисключающие фразы, ложной из них должна быть только одна. Противоречие.
Ответ: В: 4 человека, 2 лжеца
суббота, 25 сентября 2010 г.
Решение задачи Ш27 олимпиады Кенгуру 2010
Уровень: Школьник (5 и 6 класс)
Условие.
Елена, Оксана, Наталья, Петя и Вася образуют круг. По часовой стрелке в указанном порядке и в том же направлении они зачитывают считалку:
KAN-GA-ROO-OUT-GOES-YOU (на каждый слог- один ребенок). Кто оказывается под YOU - выбывает из игры, а считалка начинается сначала от следующего ребенка. Они повторяют считалку до тех пор, пока в круге не останется один ребенок. С кого нужно начать считалку, чтобы последним остался в кругу Вася?
Варианты ответа:
А:С Елены, Б:С Оксаны, В:С Натальи, Г:С Пети, Д:С Васи,
Решение
Начнём считать, к примеру, с Елены и будем отмечать, в каком порядке дети будут выбывать из круга (см. рис).

Оказывается, что в этом случае в круге останется Петя. чтобы остался Вася, стоящий следующим по часовой стрелке, начало отсчёта также надо перенести по часовой стрелке, и начать считать с Оксаны.
Ответ: Б:С Оксаны.
Условие.
Елена, Оксана, Наталья, Петя и Вася образуют круг. По часовой стрелке в указанном порядке и в том же направлении они зачитывают считалку:
KAN-GA-ROO-OUT-GOES-YOU (на каждый слог- один ребенок). Кто оказывается под YOU - выбывает из игры, а считалка начинается сначала от следующего ребенка. Они повторяют считалку до тех пор, пока в круге не останется один ребенок. С кого нужно начать считалку, чтобы последним остался в кругу Вася?
Варианты ответа:
А:С Елены, Б:С Оксаны, В:С Натальи, Г:С Пети, Д:С Васи,
Решение
Начнём считать, к примеру, с Елены и будем отмечать, в каком порядке дети будут выбывать из круга (см. рис).

Оказывается, что в этом случае в круге останется Петя. чтобы остался Вася, стоящий следующим по часовой стрелке, начало отсчёта также надо перенести по часовой стрелке, и начать считать с Оксаны.
Ответ: Б:С Оксаны.
вторник, 14 сентября 2010 г.
Решение задачи К28 олимпиады Кенгуру 2010
Уровень: Кадет, Юниор (7, 8, 9 и 10 классы)
Условие.
На рисунке нужно пройти от круга А до круга В, двигаясь по стрелкам вверх или вправо. Для каждого пути вычисляется сумма всех чисел в кругах, через которые он проходит. Сколько различных сумм можно получить?
Варианты ответа:
А:1, Б:2, В:3, Г:4, Д:5,
Решение Применим к кругам с цифрами шахматную раскраску. Тогда все круги с двойками будут белого цвета, а с единицами и тройкой - чёрного. Путь из А в В должен пройти через 2 белые и 3 чёрные клетки. Таким образом, сумма чисел на пути может быть или 1+2+3+2+1 или 1+2+1+2+1 - итого всего 2 разных значения.
Ответ: Б:2.
Условие.
На рисунке нужно пройти от круга А до круга В, двигаясь по стрелкам вверх или вправо. Для каждого пути вычисляется сумма всех чисел в кругах, через которые он проходит. Сколько различных сумм можно получить?
Варианты ответа:
А:1, Б:2, В:3, Г:4, Д:5,
Решение Применим к кругам с цифрами шахматную раскраску. Тогда все круги с двойками будут белого цвета, а с единицами и тройкой - чёрного. Путь из А в В должен пройти через 2 белые и 3 чёрные клетки. Таким образом, сумма чисел на пути может быть или 1+2+3+2+1 или 1+2+1+2+1 - итого всего 2 разных значения.
Ответ: Б:2.
суббота, 11 сентября 2010 г.
Информационные вестники олимпиады Кенгуру 2010
Центральный оргкомитет конкурса разослал региональным координаторам информационные сборники олимпиады Кенгуру 2010.
В них - условия и решения задач этого года, фотографии, которые присылали участники олимпиады, а также статистические данные по Украине в целом и по наиболее активным школам.
Сборник должен получить каждый участник конкурса, обращайтесь к своим координаторам.
В них - условия и решения задач этого года, фотографии, которые присылали участники олимпиады, а также статистические данные по Украине в целом и по наиболее активным школам.
Сборник должен получить каждый участник конкурса, обращайтесь к своим координаторам.
четверг, 9 сентября 2010 г.
Решение задачи В30 олимпиады Кенгуру 2010
Уровень: Выпускник (11 класс)
Условие. Пусть а - больший корень уравнения x2+x-1 = 0, тогда выражение a5-5a равно:
Варианты ответа:
А:-3,
Б:3,
В: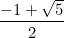 , Г:
, Г: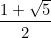 , Д:0
, Д:0
Решение
Посокльку а яввляется корнему уравнения x2+x-1 = 0, то a2 = 1-a. Значит a4 = 1-2a+a2 = 2-3a. a5-5a = a(a4-5) = a(-3-3a) = -3a-3a2 = -3a-3+3a = -3
Ответ: А:-3.
Условие. Пусть а - больший корень уравнения x2+x-1 = 0, тогда выражение a5-5a равно:
Варианты ответа:
А:-3,
Б:3,
В:
Решение
Посокльку а яввляется корнему уравнения x2+x-1 = 0, то a2 = 1-a. Значит a4 = 1-2a+a2 = 2-3a. a5-5a = a(a4-5) = a(-3-3a) = -3a-3a2 = -3a-3+3a = -3
Ответ: А:-3.
понедельник, 6 сентября 2010 г.
Решение задачи Ю16 олимпиады Кенгуру 2010
Уровень: Кадет, Юниор (7, 8, 9 и 10 класс)
Условие.
Бумажную полоску трижды перегнули пополам, а затем полностью развернули, получив на ленте семь сгибов вверх или вниз. Какое из предложенных изображений ленты нельзя получить таким способом?
Варианты ответа:
Решение:
Каждой впадине должна быть симметричная ей относительно центра ложбина. Здесь все полоски проходят по такому критерию, и каждую можно согнуть один раз. Но и у согнутой полоске должно быть такое же свойство, чтобы её можно было согнуть снова. А четвёртая полоска этому требованию не удовлетворяет: у неё и на первом, и на третьем местах по впадине.
Ответ: Г.
Условие.
Бумажную полоску трижды перегнули пополам, а затем полностью развернули, получив на ленте семь сгибов вверх или вниз. Какое из предложенных изображений ленты нельзя получить таким способом?
Варианты ответа:
Решение:
Каждой впадине должна быть симметричная ей относительно центра ложбина. Здесь все полоски проходят по такому критерию, и каждую можно согнуть один раз. Но и у согнутой полоске должно быть такое же свойство, чтобы её можно было согнуть снова. А четвёртая полоска этому требованию не удовлетворяет: у неё и на первом, и на третьем местах по впадине.
Ответ: Г.
пятница, 9 июля 2010 г.
Семинар координаторов олимпиады Кенгуру в г.Яремче
Вчера мы приехали с ежегодного семинара координаторов математической олимпиады Кенгуру, который проходил в городе Яремча Ивано-Франковской области.
Там мы встретились с математиками со всех областей Украины, прослушали несколько лекций, доклады Всеукраинского оргкомитета, предложили пакеты задачи на будущий год - и всё это на фоне живописной природы Карпат!
Развёрнутый отчёт о поездке заслуживает нескольких постов, а пока вот что можно сказать кратко:
И, в завершение первого поста, несколько фотографий местной природы:
Там мы встретились с математиками со всех областей Украины, прослушали несколько лекций, доклады Всеукраинского оргкомитета, предложили пакеты задачи на будущий год - и всё это на фоне живописной природы Карпат!
Развёрнутый отчёт о поездке заслуживает нескольких постов, а пока вот что можно сказать кратко:
- В Украине уже 480 000 участников! Такими темпами мы скоро преодолеем рубеж в полмиллиона, а если вы активно разрекламируете олимпиаду среди своих друзей, то и миллион не за горами :)
- Цена за участие в 2011 году не изменится и останется равной 10 гривен;
- Проводиться олимпиада будет в третий четверг марта, в 2011 году это будет 17е число;
- Средняя результативность участников составила около трети от максимального числа баллов. Кстати, это неплохо коррелирует с результативностью ЗНО по математике:
- С логической задачей про осьминогов справились почти 40% участников, что, в общем, неплохо. Но была одна задача, процент правильных ответов на которую был даже ниже порога угадывания. Попробуйте догадаться, какая ;)
И, в завершение первого поста, несколько фотографий местной природы:
воскресенье, 13 июня 2010 г.
Решение задачи Ю28 олимпиады Кенгуру 2010
Уровень: Кадет, Юниор (7, 8, 9 и 10 класс),
Условие
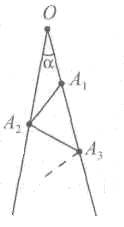
На рисунке угол a=7o, а длины отрезков ОА1, A1А2, А2А3, ... равны. Какое наибольшее количество таких отрезков (включая отрезок OA1) можно построить на этом рисунке?
Варианты ответа:
А: 10 Б:11 В: 12 Г: 13 Д: бесконечно много
Решение:

Пользуясь равенством углов при основании равнобедренного треугольника и свойством внешнего угла треугольника, находим, что углы при основания строящихся треугольников, равняются 7, 14, 21, 28 и т.д. градусов. Поскольку угол при основании не может превышать 90 градусов, и наибольшее натуральное число, не превосходящее 90, делящееся на 7, это 7*12=84, то таких треугольников может быть 12, а отрезков – 13.
Ответ:
Г: 13
Условие

На рисунке угол a=7o, а длины отрезков ОА1, A1А2, А2А3, ... равны. Какое наибольшее количество таких отрезков (включая отрезок OA1) можно построить на этом рисунке?
Варианты ответа:
А: 10 Б:11 В: 12 Г: 13 Д: бесконечно много
Решение:

Пользуясь равенством углов при основании равнобедренного треугольника и свойством внешнего угла треугольника, находим, что углы при основания строящихся треугольников, равняются 7, 14, 21, 28 и т.д. градусов. Поскольку угол при основании не может превышать 90 градусов, и наибольшее натуральное число, не превосходящее 90, делящееся на 7, это 7*12=84, то таких треугольников может быть 12, а отрезков – 13.
Ответ:
Г: 13
вторник, 8 июня 2010 г.
Решение задачи В27 олимпиады Кенгуру 2010
Уровень: Выпускник (11 класс)
Условие
Бумажную полоску сложили так, как это показано на рисунке. Найдите угол , если
, если 

Варианты ответа:
А: 140o Б:130o В: 120o Г: 110o Д: 100o
Решение:
Совместим второе и четвёртое положения полоски. Все четыре отмеченные дугами угла будут равны. Между собой. Каждый из них будет равняться

Так что

Ответ: В: 120o
Условие
Бумажную полоску сложили так, как это показано на рисунке. Найдите угол

Варианты ответа:
А: 140o Б:130o В: 120o Г: 110o Д: 100o
Решение:
Совместим второе и четвёртое положения полоски. Все четыре отмеченные дугами угла будут равны. Между собой. Каждый из них будет равняться

Так что
Ответ: В: 120o
суббота, 5 июня 2010 г.
Решение задачи Ю26 олимпиады Кенгуру 2010
Уровень: Юниор (9 и 10 класс)
Условие
Сколько существует трехзначных чисел, у которых вторая цифра является средним арифметическим двух других?
Варианты ответа:
А: 16 Б: 20 В: 25 Г: 36 Д: 45
Решение:
Поскольку вторая цифра числа является средним арифметическим двух других, то сумма двух других цифр равна удвоенной второй цифре. Тогда могут быть такие варианты:
Вторая цифра равна 1:
2+0=1+1=2 – два варианта чисел с единицей в середине.
Вторая цифра равна 2:
3+0=3+1=2+2=1+3=4 – четыре варианта для чисел со второй цифрой – двойкой.
Вторая цифра равна 3:
6+0=5+1=4+2=3+3=2+4=1+5=6 – 6 вариантов
Вторая цифра равна 4:
8+0=7+1=6+2=5+3=4+4=3+5=2+6=1+7=8 – 8 вариантов
Вторая цифра равна 5:
9+1=8+2=7+3=6+4=5+5=4+6=3+7=2+8=1+9 – 9 вариантов
Далее будет по 7, 5, 3, 2 и 1 варианту для случаев второй цифры, равной 6, 7, 8 и 9, соответственно.
Всего чисел, удовлетворяющих условию, будет 2+4+6+8+9+7+5+3+1=45.
Ответ: Д: 45
Условие
Сколько существует трехзначных чисел, у которых вторая цифра является средним арифметическим двух других?
Варианты ответа:
А: 16 Б: 20 В: 25 Г: 36 Д: 45
Решение:
Поскольку вторая цифра числа является средним арифметическим двух других, то сумма двух других цифр равна удвоенной второй цифре. Тогда могут быть такие варианты:
Вторая цифра равна 1:
2+0=1+1=2 – два варианта чисел с единицей в середине.
Вторая цифра равна 2:
3+0=3+1=2+2=1+3=4 – четыре варианта для чисел со второй цифрой – двойкой.
Вторая цифра равна 3:
6+0=5+1=4+2=3+3=2+4=1+5=6 – 6 вариантов
Вторая цифра равна 4:
8+0=7+1=6+2=5+3=4+4=3+5=2+6=1+7=8 – 8 вариантов
Вторая цифра равна 5:
9+1=8+2=7+3=6+4=5+5=4+6=3+7=2+8=1+9 – 9 вариантов
Далее будет по 7, 5, 3, 2 и 1 варианту для случаев второй цифры, равной 6, 7, 8 и 9, соответственно.
Всего чисел, удовлетворяющих условию, будет 2+4+6+8+9+7+5+3+1=45.
Ответ: Д: 45
пятница, 28 мая 2010 г.
Решение задачи К25 олимпиады Кенгуру 2010
Уровень: Кадет (7 и 8 класс)
Условие
На доске выписаны натуральные числа от 1 до 10. Ваня вытирает любые два из этих чисел, а вместо них записывает их сумму, уменьшенную на единицу. Эту процедуру мальчик повторяет, пока на доске не останется только одно число. Какое?
Варианты ответа:
А: меньшее, чем 11 Б: 11 В: 46 Г: большее, чем 46 Д: другой ответ
Решение:
C каждой такой операцией сумма всех чисел на доске уменьшается на единицу. Вначале сумма всех чисел на доске равна 55. После девяти сложений она составит 46.
Ответ: В: 46
четверг, 27 мая 2010 г.
среда, 26 мая 2010 г.
Решение задачи Ш24 олимпиады Кенгуру 2010
Уровень: Школьник (5 и 6 класс)
Условие
Иван, написав двузначное число, приписывает к нему справа сумму его цифр. Например, 12 —> 123, или 29 —> 2911. Затем он повторяет эту операцию для двух последних цифр полученного числа и т. д. Например, 12 —> 123 —> 1235 —> 12358 —> 1235813 —> и т.д. Если Иван начнет с числа 31, то какой будет 2010-я цифра?
Варианты ответа:
А: 1 Б: 4 В: 5 Г: 8 Д: 9
Решение:
Сделаем несколько шагов
31->314->3145->31459->3145914->31459145->314591459
Уже можно видеть, что в получающемся числе будет повторяться группа цифр (1459). Т.к. период начинается после первой цифры, а число 2009=2010-1 даёт остаток 1 при делении на 4, то 2010 цифрой будет первая цифра периода, т.е. единица.
Ответ: А: 1
P.S. Интересным развитием этой задачи было бы нахождения такого двузначного числа, которое дало бы при выполнении указанной операции период наибольшей длины.
Условие
Иван, написав двузначное число, приписывает к нему справа сумму его цифр. Например, 12 —> 123, или 29 —> 2911. Затем он повторяет эту операцию для двух последних цифр полученного числа и т. д. Например, 12 —> 123 —> 1235 —> 12358 —> 1235813 —> и т.д. Если Иван начнет с числа 31, то какой будет 2010-я цифра?
Варианты ответа:
А: 1 Б: 4 В: 5 Г: 8 Д: 9
Решение:
Сделаем несколько шагов
31->314->3145->31459->3145914->31459145->314591459
Уже можно видеть, что в получающемся числе будет повторяться группа цифр (1459). Т.к. период начинается после первой цифры, а число 2009=2010-1 даёт остаток 1 при делении на 4, то 2010 цифрой будет первая цифра периода, т.е. единица.
Ответ: А: 1
P.S. Интересным развитием этой задачи было бы нахождения такого двузначного числа, которое дало бы при выполнении указанной операции период наибольшей длины.
понедельник, 24 мая 2010 г.
Решение задачи Ш22 олимпиады Кенгуру 2010
Уровень: Школьник (5 и 6 класс)
Условие
Сергей с друзьями поровну разделили между собой некоторое количество яблок. Когда к ним подошел Петр, все решили разделить яблоки по-новому: поровну, включая Петра. После раздела Сергей заметил, что получил на шестую часть яблок меньше, чем вначале. Сколько друзей, вместе с Сергеем, собрались сначала?
Варианты ответа:
А: 2 Б: 3 В: 4 Г: 5 Д: 6
Решение:
Куда делась шестая часть яблок Сергея? Разумеется, перешла Петру. Петру же перешли шестые части долей всех остальных ребят. Значит, Пётр получил шестую часть всех яблок и вместе с Петром друзей было шестеро. Сначала же их собралось пятеро.
Ответ: Г: 5
Условие
Сергей с друзьями поровну разделили между собой некоторое количество яблок. Когда к ним подошел Петр, все решили разделить яблоки по-новому: поровну, включая Петра. После раздела Сергей заметил, что получил на шестую часть яблок меньше, чем вначале. Сколько друзей, вместе с Сергеем, собрались сначала?
Варианты ответа:
А: 2 Б: 3 В: 4 Г: 5 Д: 6
Решение:
Куда делась шестая часть яблок Сергея? Разумеется, перешла Петру. Петру же перешли шестые части долей всех остальных ребят. Значит, Пётр получил шестую часть всех яблок и вместе с Петром друзей было шестеро. Сначала же их собралось пятеро.
Ответ: Г: 5
суббота, 22 мая 2010 г.
Задача К21 олимпиады по математике Кенгуру 2010, решение и ответ
Уровень: Кадет (7 и 8 класс)
Условие

На рисунке изображены девять областей, ограниченных дугами окружностей. В каждую область в каком-то порядке записано по одному числу от 1 до 9 (каждое число по одному разу) так, что сумма чисел внутри каждого круга равна 11. Какое число записано в область, отмеченную знаком вопроса?
Варианты ответа:
А: 5 Б: 6 В: 7 Г: 8 Д: 9
Решение:
Число 11 можно представить в виде трёх разных слагаемых от 1 до 9 девятью способами.
11=9+2=8+3=8+2+1=7+4=7+3+1=6+5=6+4+1=6+3+2=5+4+2
Девятка входит только в одну сумму, значит, уже можно определить положение девятки и двойки.

Сумма цифр, лежащих в двух нижних кругах, равна 22. Т.к. сумма всех цифр равна 45, то сумма крайней левой, центральной и крайней правой цифр равна 45-22=23. Значит, сумма левой и центральной цифр равна 23-9=14.
Получается, на месте знака вопроса стоит или 6 или 8. Но единственная сумма из трёх слагаемых, куда входит восьмёрка – это 1+2+8, а место для двойки занято. Поэтому восьмёрка – крайне правая цифра, и на месте знака вопроса стоит цифра 6.
Ответ: Б: 6
Условие

На рисунке изображены девять областей, ограниченных дугами окружностей. В каждую область в каком-то порядке записано по одному числу от 1 до 9 (каждое число по одному разу) так, что сумма чисел внутри каждого круга равна 11. Какое число записано в область, отмеченную знаком вопроса?
Варианты ответа:
А: 5 Б: 6 В: 7 Г: 8 Д: 9
Решение:
Число 11 можно представить в виде трёх разных слагаемых от 1 до 9 девятью способами.
11=9+2=8+3=8+2+1=7+4=7+3+1=6+5=6+4+1=6+3+2=5+4+2
Девятка входит только в одну сумму, значит, уже можно определить положение девятки и двойки.

Сумма цифр, лежащих в двух нижних кругах, равна 22. Т.к. сумма всех цифр равна 45, то сумма крайней левой, центральной и крайней правой цифр равна 45-22=23. Значит, сумма левой и центральной цифр равна 23-9=14.
Получается, на месте знака вопроса стоит или 6 или 8. Но единственная сумма из трёх слагаемых, куда входит восьмёрка – это 1+2+8, а место для двойки занято. Поэтому восьмёрка – крайне правая цифра, и на месте знака вопроса стоит цифра 6.
Ответ: Б: 6
понедельник, 17 мая 2010 г.
Прибыли результаты олимпиады Кенгуру по Кировоградской области
Результаты конкурса Кенгуру 2010 по Кировоградской области и дипломы - у координатора области. С завтрашнего дня начинается рассылка по районам.
Задача Ю20 олимпиады по математике Кенгуру 2010
Уровень: Юниор, Школьник (5, 6, 9 и 10 класс)
Условие
У подводного царя служат осьминоги с шестью, семью или восемью ногами. Те, у кого 7 ног, всегда врут, а те, у кого 6 или 8 ног, - всегда говорят правду. Встретились четыре осьминога. Синий сказал: "Вместе у нас 28 ног", зеленый: "Вместе у нас 27 ног", желтый: "Вместе у нас 26 ног", красный: "Вместе у нас 25 ног". Какого цвета осьминог, сказавший правду?
Варианты ответа:
А: красный Б: синий В: зеленый Г: желтый Д: ни один осьминог не сказал правду
Решение
Поскольку все реплики были различными, солгали 3 или 4 осьминога. Если бы соврали четверо, то у них должно было быть 7х4=28 ног. Но в таком случае фраза "Вместе у нас 28 ног" была бы правдой. Противоречие.
Значит, соврали трое, а один сказал правду. Тогда у четверых осьминогов могло быть или 3х7+6=27 или 3х7+8=29 ног. Поэтому правдой была фраза зелёного "Вместе у нас 27 ног"
Ответ: В: зеленый
Условие
У подводного царя служат осьминоги с шестью, семью или восемью ногами. Те, у кого 7 ног, всегда врут, а те, у кого 6 или 8 ног, - всегда говорят правду. Встретились четыре осьминога. Синий сказал: "Вместе у нас 28 ног", зеленый: "Вместе у нас 27 ног", желтый: "Вместе у нас 26 ног", красный: "Вместе у нас 25 ног". Какого цвета осьминог, сказавший правду?
Варианты ответа:
А: красный Б: синий В: зеленый Г: желтый Д: ни один осьминог не сказал правду
Решение
Поскольку все реплики были различными, солгали 3 или 4 осьминога. Если бы соврали четверо, то у них должно было быть 7х4=28 ног. Но в таком случае фраза "Вместе у нас 28 ног" была бы правдой. Противоречие.
Значит, соврали трое, а один сказал правду. Тогда у четверых осьминогов могло быть или 3х7+6=27 или 3х7+8=29 ног. Поэтому правдой была фраза зелёного "Вместе у нас 27 ног"
Ответ: В: зеленый
воскресенье, 16 мая 2010 г.
Задача В19 олимпиады по математике Кенгуру 2010
Уровень: Выпускник (11 класс)
Условие

На рисунке изображены графики функций=\sqrt{1-x^2}) и
и =1-\sqrt{2x-x^2}) ..
..
Значение-g(x)\right) \text{d}x) равно:
равно:
Варианты ответа:
А: Б:
Б:  В:
В:  Г:
Г:  Д:
Д: 
Решение
Проведём отрезки, как показано на рисунке:

Искомый интеграл равен площади двух круговых сегментов. А их площадь, в свою очередь, равна разности между площадью полукруга радиусом 1 и квадрата со стороной 1. Так что-g(x)\right) \text{d}x=\frac{\pi}{2}-1=\frac{\pi-2}{2})
Ответ: Г:
Условие

На рисунке изображены графики функций
Значение
Варианты ответа:
А:
Решение
Проведём отрезки, как показано на рисунке:

Искомый интеграл равен площади двух круговых сегментов. А их площадь, в свою очередь, равна разности между площадью полукруга радиусом 1 и квадрата со стороной 1. Так что
Ответ: Г:
пятница, 14 мая 2010 г.
Результаты олимпиады Кенгуру - уже скоро!
Сегодня координатор конкурса в Украине Андрей Добосевич сообщил нам, что дипломы и таблицы результатов отправлены в регионы. Так что на днях они будут у региональных координаторов.
Задача Ю18 олимпиады по математике Кенгуру 2010
Уровень: Юниор (9 и 10 класс)
Условие

На диаграмме изображена зависимость между расстоянием и временем, за которое это расстояние пробежал каждый из пяти школьников. Кто из них был самым быстрым?
Варианты ответа:
А: Андрей Б: Василий В: Марийка Г: Николай Д: Елена
Решение
Т.к. скорость – это отношение пройденного расстояния к затраченному времени, соединим результаты каждого из бегунов с началом координат. Самым быстрым был тот, у кого соответствующий отрезок .наклонён под наибольшим углом к оси времени. Значит, это был Андрей.

Ответ: А: Андрей
Условие

На диаграмме изображена зависимость между расстоянием и временем, за которое это расстояние пробежал каждый из пяти школьников. Кто из них был самым быстрым?
Варианты ответа:
А: Андрей Б: Василий В: Марийка Г: Николай Д: Елена
Решение
Т.к. скорость – это отношение пройденного расстояния к затраченному времени, соединим результаты каждого из бегунов с началом координат. Самым быстрым был тот, у кого соответствующий отрезок .наклонён под наибольшим углом к оси времени. Значит, это был Андрей.

Ответ: А: Андрей
среда, 12 мая 2010 г.
Задача К17 олимпиады по математике Кенгуру 2010
Уровень: Кадет (7 и 8 класс)
Условие

На рисунке изображен прямоугольник ABCD и квадрат PQRS. Площадь затемнённой фигуры равна половине площади прямоугольника ABCD. Тогда длина отрезка РХ равна:
Варианты ответа:
А: 1 Б: 1,5 В:2 Г: 2,5 Д:4
Решение
Площадь прямоугольника ABCD равна 60. Значит площадь прямоугольника SXYR должна равняться 30. Поскольку сторона SR = 6, то XS=5 и PX = PS-XS=1.
Ответ: А: 1
Условие

На рисунке изображен прямоугольник ABCD и квадрат PQRS. Площадь затемнённой фигуры равна половине площади прямоугольника ABCD. Тогда длина отрезка РХ равна:
Варианты ответа:
А: 1 Б: 1,5 В:2 Г: 2,5 Д:4
Решение
Площадь прямоугольника ABCD равна 60. Значит площадь прямоугольника SXYR должна равняться 30. Поскольку сторона SR = 6, то XS=5 и PX = PS-XS=1.
Ответ: А: 1
четверг, 6 мая 2010 г.
Задача В2 олимпиады по математике Кенгуру 2010
Уровень: Выпускник, Юниор (9, 10 и 11 класс)
Условие
Если суммы чисел в обеих строках таблицы одинаковы, то число, обозначенное звёздочкой (*), равно:
Варианты ответа:
А: 1010 Б: 1020 В: 1910 Г: 1990 Д: 2000
Решение
Можно заметить, что числа в десяти нижних ячейках на 10 больше соответствующих чисел в верхних ячейках. Значит сумма чисел в десяти нижних ячейках на 100 больше суммы чисел в десяти соответствующих чисел в верхних ячейках. Чтобы суммы по строкам были равными, вместо звёздочки должно стоять число, на 100 меньшее, чем 2010, т.е. 2010-100=1910
Ответ: В: 1910
Уровень: Школьник (5 и 6 класс)
Условие
Если суммы чисел в обеих строках таблицы одинаковы, то число, обозначенное звёздочкой (*), равно:
Варианты ответа:
А: 99 Б: 100 В: 209 Г: 289 Д: 299
Решение
Аналогичными рассуждениями находим, что вместо звёздочки должно стоять число, на 100 меньшее, чем 199, т.е. 99
Ответ: А: 99
Уровень: Малыш 3-4 (3 и 4 класс)
Условие
Если суммы чисел в обеих строках таблицы одинаковы, то число, обозначенное звёздочкой (*), равно:
Варианты ответа:
А: 7 Б: 10 В: 17 Г: 59 Д: 70
Решение
Здесь чтобы суммы сравнялись, нужно вместо звёздочки поставить число на 60 меньшее семидесяти, т.е. 10
Ответ: Б: 10
Уровень: Малыш 2 (2 класс)
Условие
Если суммы чисел в обеих строках одинаковы, то какое число стоит сместо звёздочки?
Варианты ответа:
А: 4 Б: 10 В: 13 Г: 22 Д: 43
Решение
Аналогично предыдущим задачам, там должно стоять 40-30=10
Ответ: Б: 10
Условие
| 1 | 2 | 3 | 4 | 5 | б | 7 | 8 | 9 | 10 | 2010 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | * |
Варианты ответа:
А: 1010 Б: 1020 В: 1910 Г: 1990 Д: 2000
Решение
Можно заметить, что числа в десяти нижних ячейках на 10 больше соответствующих чисел в верхних ячейках. Значит сумма чисел в десяти нижних ячейках на 100 больше суммы чисел в десяти соответствующих чисел в верхних ячейках. Чтобы суммы по строкам были равными, вместо звёздочки должно стоять число, на 100 меньшее, чем 2010, т.е. 2010-100=1910
Ответ: В: 1910
Уровень: Школьник (5 и 6 класс)
Условие
| 1 | 2 | 3 | 4 | 5 | б | 7 | 8 | 9 | 10 | 199 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | * |
Варианты ответа:
А: 99 Б: 100 В: 209 Г: 289 Д: 299
Решение
Аналогичными рассуждениями находим, что вместо звёздочки должно стоять число, на 100 меньшее, чем 199, т.е. 99
Ответ: А: 99
Уровень: Малыш 3-4 (3 и 4 класс)
Условие
| 1 | 2 | 3 | 4 | 5 | 6 | 70 |
| 11 | 12 | 13 | 14 | 15 | 16 | * |
Варианты ответа:
А: 7 Б: 10 В: 17 Г: 59 Д: 70
Решение
Здесь чтобы суммы сравнялись, нужно вместо звёздочки поставить число на 60 меньшее семидесяти, т.е. 10
Ответ: Б: 10
Уровень: Малыш 2 (2 класс)
Условие
| 1 | 2 | 3 | 40 |
| 11 | 12 | 13 | * |
Варианты ответа:
А: 4 Б: 10 В: 13 Г: 22 Д: 43
Решение
Аналогично предыдущим задачам, там должно стоять 40-30=10
Ответ: Б: 10
понедельник, 3 мая 2010 г.
Задача М(3-4)15 олимпиады по математике Кенгуру 2010
Уровень: Малыш 3-4, Малыш 2 (2, 3 и 4 класс)
Условие
Дети решили измерить длину площадки шагами. Олег прошел вдоль площадки, сделав 15 шагов, Богдан - 17, Денис - 12, а Игорь - 14 шагов. Чьи шаги были самыми длинными?
Варианты ответа:
А: Олега Б: Богдана В: Дениса Г: Игоря Д: Невозможно определить
Решение
Чем шаги длиннее, тем меньше их нужно, чтобы пройти через площадку. Поэтому шаги Дениса были самыми длинными.
Ответ: В: Дениса
Условие
Дети решили измерить длину площадки шагами. Олег прошел вдоль площадки, сделав 15 шагов, Богдан - 17, Денис - 12, а Игорь - 14 шагов. Чьи шаги были самыми длинными?

Варианты ответа:
А: Олега Б: Богдана В: Дениса Г: Игоря Д: Невозможно определить
Решение
Чем шаги длиннее, тем меньше их нужно, чтобы пройти через площадку. Поэтому шаги Дениса были самыми длинными.
Ответ: В: Дениса
пятница, 30 апреля 2010 г.
Задача Ш14 олимпиады по математике Кенгуру 2010
Уровень: Школьник, Малыш 3-4 (3, 4, 5 и 6 класс)
Условие

Числа 1, 4, 7, 10 и 13 нужно записать в ячейки этой фигуры так, чтобы сумма чисел в строке равнялась сумме чисел в столбце. Чему равна наибольшая такая сумма?
Варианты ответа:
А: 18 Б: 20 В: 21 Г: 22 Д: 24
Решение
Нужно среди данных чисел выбрать две пары, дающие равные суммы. Тогда они запишутся в крайние ячейки, а в центральную попадёт оставшееся число. Из трёх возможных вариантов наибольшую сумму, равную 24 даст такое расположение:

Ответ: Д: 24
Уровень: Малыш 2 (2 класс)
Условие
Числа 1, 4, 10 и 13 нужно записать в ячейки этой фигуры так, чтобы сумма чисел в строке равнялась сумме чисел в столбце. Чему равна такая сумма?

Варианты ответа:
А: 5 Б: 11 В: 15 Г: 21 Д: 23
Решение
Числа 1, 4, 10 и 13 можно разбить на пары 1+13=4+10. Числа из этих пар нужно будет записать в противоположные ячейки. Тогда суммы в строке и столбце будут равны 1+13+7=21.
Ответ: Г: 21
Условие

Числа 1, 4, 7, 10 и 13 нужно записать в ячейки этой фигуры так, чтобы сумма чисел в строке равнялась сумме чисел в столбце. Чему равна наибольшая такая сумма?
Варианты ответа:
А: 18 Б: 20 В: 21 Г: 22 Д: 24
Решение
Нужно среди данных чисел выбрать две пары, дающие равные суммы. Тогда они запишутся в крайние ячейки, а в центральную попадёт оставшееся число. Из трёх возможных вариантов наибольшую сумму, равную 24 даст такое расположение:

Ответ: Д: 24
Уровень: Малыш 2 (2 класс)
Условие
Числа 1, 4, 10 и 13 нужно записать в ячейки этой фигуры так, чтобы сумма чисел в строке равнялась сумме чисел в столбце. Чему равна такая сумма?

Варианты ответа:
А: 5 Б: 11 В: 15 Г: 21 Д: 23
Решение
Числа 1, 4, 10 и 13 можно разбить на пары 1+13=4+10. Числа из этих пар нужно будет записать в противоположные ячейки. Тогда суммы в строке и столбце будут равны 1+13+7=21.
Ответ: Г: 21
Подписаться на:
Сообщения (Atom)