Условие
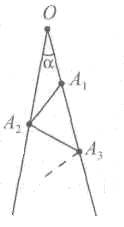
На рисунке угол a=7o, а длины отрезков ОА1, A1А2, А2А3, ... равны. Какое наибольшее количество таких отрезков (включая отрезок OA1) можно построить на этом рисунке?
Варианты ответа:
А: 10 Б:11 В: 12 Г: 13 Д: бесконечно много
Решение:

Пользуясь равенством углов при основании равнобедренного треугольника и свойством внешнего угла треугольника, находим, что углы при основания строящихся треугольников, равняются 7, 14, 21, 28 и т.д. градусов. Поскольку угол при основании не может превышать 90 градусов, и наибольшее натуральное число, не превосходящее 90, делящееся на 7, это 7*12=84, то таких треугольников может быть 12, а отрезков – 13.
Ответ:
Г: 13
Комментариев нет:
Отправить комментарий