Решение задачи про дни рождения

Уровень: Кадет, Малыш 3-4 (3, 4, 7 и 8 классы),
Условие. Виталик сложил числа дней и числа месяцев дат рождения всех своих друзей и получил 35. Даты рождения его друзей различны. Какое наибольшее возможное количество друзей у Виталика?
Варианты ответа: А:7, Б:8, В:9, Г:10, Д:12,

Решение Понятно, что наибольшее число друзей будет, если суммы чисел в их датах рождения минимальны. Сумма 2 будет у родившегося 1 января, Сумма 3 - у родившихся 1 февраля и 2 января, сумма 4 - у 3 января, 2 февраля и 1 марта. Для этих 6 человек сумма чисел дней и месяцев рождения составит 2+3+3+4+4+4=20. Добавим ещё трёх человек с суммой 5: 4 января, 3 февраля и 2 марта. Итого 9 друзей.

Ответ: В:9

Решение задачи про степени (Ю23)

Уровень: Юниор (9 и 10 класс)
Условие. Для скольких натуральных чисел n от 1 до 100 включительно число nⁿ является квадратом натурального числа?

Варианты ответа: А:5, Б:15, В:50, Г:54, Д:55,

Решение Во-первых, квадратом nⁿ будет для чётного n. Таких чисел от 1 до 100 будет 50. Во-вторых, для нечётного n, являющегося квадратом. Таких n будет 5: 1, 9, 25, 49, 81. Итого 55 вариантов.

Ответ: Д:55

Аналогичная, но более сложная задача сейчас сдерживает наступление на Хребет натуральных чисел в игре Математические маневры.

Решение задачи про квадрат (Ш19) олимпиады Кенгуру 2010

Уровень: Школьник (5 и 6 класс)
Условие.

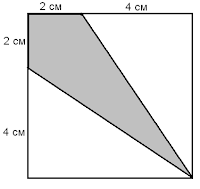
Вычислите площадь затемненной части квадрата


Варианты ответа: А:8 см², Б:12 см², В:18 см², Г:24 см², Д:36 см²

Решение
Разобьём этот квадрат диагональю, являющейся осью симметрии затемнённой фигуры. Тогда фигура разобьётся на два треугольника с основаниями 2 см, и высотами 6 см. Площадь одного такого треугольника равна 6 см², а всей фигуры 12 см²

Ответ: Б:12 см².

Решение задачи про последовательность (Ю25)

Уровень: Юниор (9  и 10 класс)

Условие. Первый, второй и третий члены последовательности равны соответственно 1, 2 и 3. Каждый последующий член последовательности, начиная с четвертого,
определяется по формуле а_n = a_n-3 + а_n-2 - а_n-1, n Є N , n > 3 . Тогда а₂₀₁₀ =

Варианты ответа:
А:-2010, Б:-2006, В:2002, Г:2009, Д:2010,

Решение
Получим несоклько членов этой последовательности:
1, 2, 3, 0, 5, -2, 7, -4, 9, -6, …
Замечаем, что последовталеьность распадается на две. Её члены с нечётными номерами равны своему номеру, а с чётными a_2n=4-2n.

Докажем это по индукции. Пyсть для всех n, меньших k a_2n=2-2n и a_2n+1=2n+1. 

Тогда a_2k+2 = a_2k-1 + a_2k - a_2k+1 = 2k-1 + 4-2k – (2k+1) = 4-(2k+2)
a_2k+3 = a_2k + a_2k+1 - a_2k+2 = 4-2k + 2k+1 – (4-(2k+2)) = 2k+3

Значит a₂₀₁₀ = 4-2010 = -2006

Ответ:Б:-2006