Уровень: Кадет (7 и 8 класс)
Условие. В городе Буле некоторые жители - лжецы, и они всегда врут, а все остальные всегда говорят правду. Однажды в одной комнате находилось несколько жителей этого города, и трое из них сказали следующее:
1) Нас здесь не более трех человек. Все мы - лжецы.
2) Нас здесь не более четырех человек. Не все мы лжецы.
3) Нас тут пятеро. Трое из нас лжецы.
Определите, сколько в комнате людей и сколько среди них лжецов.
Варианты ответа:
А: 3 человека, 1 лжец, Б: 4 человека, 1 лжец, В: 4 человека, 2 лжеца, Г: 5 человек, 2 лжеца, Д: 5 человек, 3 лжеца,
Решение Допустим, в комнате трое. Тогда первая фраза первого человека "Нас здесь не более трех человек" - истинна. Тогда должна быть истинной и вторая его фраза "Все мы - лжецы". Но она истинной быть не может. Значит, человек в комнате больше трёх.
Допустим, в комнате четверо. Тогда первый человек сказал неправду. Второй, соответственно, правду. А третий солгал. Значит, два лжеца уже есть (это первый и третий). А троих лжецов быть не может, поскольку третий солгал, сказав "Трое из нас лжецы". Так что ответ "4 человека, 2 лжеца" непротиворечив.
Ответ найден, но для интереса проверим, могло ли в комнате быть пятеро. В таком случае первые двое соврали. Значит, ложны их фразы "Все мы - лжецы" и "Не все мы лжецы". А т.к. это взаимоисключающие фразы, ложной из них должна быть только одна. Противоречие.
Ответ: В: 4 человека, 2 лжеца
Всё, что касается подготовки, проведения и результатов олимпиады.
среда, 29 сентября 2010 г.
суббота, 25 сентября 2010 г.
Решение задачи Ш27 олимпиады Кенгуру 2010
Уровень: Школьник (5 и 6 класс)
Условие.
Елена, Оксана, Наталья, Петя и Вася образуют круг. По часовой стрелке в указанном порядке и в том же направлении они зачитывают считалку:
KAN-GA-ROO-OUT-GOES-YOU (на каждый слог- один ребенок). Кто оказывается под YOU - выбывает из игры, а считалка начинается сначала от следующего ребенка. Они повторяют считалку до тех пор, пока в круге не останется один ребенок. С кого нужно начать считалку, чтобы последним остался в кругу Вася?
Варианты ответа:
А:С Елены, Б:С Оксаны, В:С Натальи, Г:С Пети, Д:С Васи,
Решение
Начнём считать, к примеру, с Елены и будем отмечать, в каком порядке дети будут выбывать из круга (см. рис).

Оказывается, что в этом случае в круге останется Петя. чтобы остался Вася, стоящий следующим по часовой стрелке, начало отсчёта также надо перенести по часовой стрелке, и начать считать с Оксаны.
Ответ: Б:С Оксаны.
Условие.
Елена, Оксана, Наталья, Петя и Вася образуют круг. По часовой стрелке в указанном порядке и в том же направлении они зачитывают считалку:
KAN-GA-ROO-OUT-GOES-YOU (на каждый слог- один ребенок). Кто оказывается под YOU - выбывает из игры, а считалка начинается сначала от следующего ребенка. Они повторяют считалку до тех пор, пока в круге не останется один ребенок. С кого нужно начать считалку, чтобы последним остался в кругу Вася?
Варианты ответа:
А:С Елены, Б:С Оксаны, В:С Натальи, Г:С Пети, Д:С Васи,
Решение
Начнём считать, к примеру, с Елены и будем отмечать, в каком порядке дети будут выбывать из круга (см. рис).

Оказывается, что в этом случае в круге останется Петя. чтобы остался Вася, стоящий следующим по часовой стрелке, начало отсчёта также надо перенести по часовой стрелке, и начать считать с Оксаны.
Ответ: Б:С Оксаны.
вторник, 14 сентября 2010 г.
Решение задачи К28 олимпиады Кенгуру 2010
Уровень: Кадет, Юниор (7, 8, 9 и 10 классы)
Условие.
На рисунке нужно пройти от круга А до круга В, двигаясь по стрелкам вверх или вправо. Для каждого пути вычисляется сумма всех чисел в кругах, через которые он проходит. Сколько различных сумм можно получить?
Варианты ответа:
А:1, Б:2, В:3, Г:4, Д:5,
Решение Применим к кругам с цифрами шахматную раскраску. Тогда все круги с двойками будут белого цвета, а с единицами и тройкой - чёрного. Путь из А в В должен пройти через 2 белые и 3 чёрные клетки. Таким образом, сумма чисел на пути может быть или 1+2+3+2+1 или 1+2+1+2+1 - итого всего 2 разных значения.
Ответ: Б:2.
Условие.
На рисунке нужно пройти от круга А до круга В, двигаясь по стрелкам вверх или вправо. Для каждого пути вычисляется сумма всех чисел в кругах, через которые он проходит. Сколько различных сумм можно получить?
Варианты ответа:
А:1, Б:2, В:3, Г:4, Д:5,
Решение Применим к кругам с цифрами шахматную раскраску. Тогда все круги с двойками будут белого цвета, а с единицами и тройкой - чёрного. Путь из А в В должен пройти через 2 белые и 3 чёрные клетки. Таким образом, сумма чисел на пути может быть или 1+2+3+2+1 или 1+2+1+2+1 - итого всего 2 разных значения.
Ответ: Б:2.
суббота, 11 сентября 2010 г.
Информационные вестники олимпиады Кенгуру 2010
Центральный оргкомитет конкурса разослал региональным координаторам информационные сборники олимпиады Кенгуру 2010.
В них - условия и решения задач этого года, фотографии, которые присылали участники олимпиады, а также статистические данные по Украине в целом и по наиболее активным школам.
Сборник должен получить каждый участник конкурса, обращайтесь к своим координаторам.
В них - условия и решения задач этого года, фотографии, которые присылали участники олимпиады, а также статистические данные по Украине в целом и по наиболее активным школам.
Сборник должен получить каждый участник конкурса, обращайтесь к своим координаторам.
четверг, 9 сентября 2010 г.
Решение задачи В30 олимпиады Кенгуру 2010
Уровень: Выпускник (11 класс)
Условие. Пусть а - больший корень уравнения x2+x-1 = 0, тогда выражение a5-5a равно:
Варианты ответа:
А:-3,
Б:3,
В: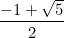 , Г:
, Г: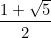 , Д:0
, Д:0
Решение
Посокльку а яввляется корнему уравнения x2+x-1 = 0, то a2 = 1-a. Значит a4 = 1-2a+a2 = 2-3a. a5-5a = a(a4-5) = a(-3-3a) = -3a-3a2 = -3a-3+3a = -3
Ответ: А:-3.
Условие. Пусть а - больший корень уравнения x2+x-1 = 0, тогда выражение a5-5a равно:
Варианты ответа:
А:-3,
Б:3,
В:
Решение
Посокльку а яввляется корнему уравнения x2+x-1 = 0, то a2 = 1-a. Значит a4 = 1-2a+a2 = 2-3a. a5-5a = a(a4-5) = a(-3-3a) = -3a-3a2 = -3a-3+3a = -3
Ответ: А:-3.
понедельник, 6 сентября 2010 г.
Решение задачи Ю16 олимпиады Кенгуру 2010
Уровень: Кадет, Юниор (7, 8, 9 и 10 класс)
Условие.
Бумажную полоску трижды перегнули пополам, а затем полностью развернули, получив на ленте семь сгибов вверх или вниз. Какое из предложенных изображений ленты нельзя получить таким способом?
Варианты ответа:
Решение:
Каждой впадине должна быть симметричная ей относительно центра ложбина. Здесь все полоски проходят по такому критерию, и каждую можно согнуть один раз. Но и у согнутой полоске должно быть такое же свойство, чтобы её можно было согнуть снова. А четвёртая полоска этому требованию не удовлетворяет: у неё и на первом, и на третьем местах по впадине.
Ответ: Г.
Условие.
Бумажную полоску трижды перегнули пополам, а затем полностью развернули, получив на ленте семь сгибов вверх или вниз. Какое из предложенных изображений ленты нельзя получить таким способом?
Варианты ответа:
Решение:
Каждой впадине должна быть симметричная ей относительно центра ложбина. Здесь все полоски проходят по такому критерию, и каждую можно согнуть один раз. Но и у согнутой полоске должно быть такое же свойство, чтобы её можно было согнуть снова. А четвёртая полоска этому требованию не удовлетворяет: у неё и на первом, и на третьем местах по впадине.
Ответ: Г.
Подписаться на:
Комментарии (Atom)


