Задача Ш14 олимпиады по математике Кенгуру 2010

Уровень: Школьник, Малыш 3-4  (3, 4, 5 и 6 класс)
Условие




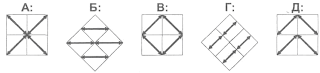
Числа 1, 4, 7, 10 и 13 нужно записать в ячейки этой фигуры так, чтобы сумма чисел в строке равнялась сумме чисел в столбце. Чему равна наибольшая такая сумма?
Варианты ответа:

А: 18 Б: 20 В: 21 Г: 22 Д: 24

Решение
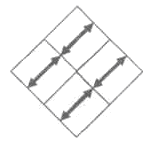
Нужно среди данных чисел выбрать две пары, дающие равные суммы. Тогда они запишутся в крайние ячейки, а в центральную попадёт оставшееся число. Из трёх возможных вариантов наибольшую сумму, равную 24 даст такое расположение:



Ответ: Д: 24

Уровень: Малыш 2  (2 класс)

Условие

Числа 1, 4, 10 и 13 нужно записать в ячейки этой  фигуры так, чтобы сумма чисел в строке равнялась сумме чисел в столбце. Чему равна такая сумма?

Варианты ответа:

А: 5 Б: 11 В: 15 Г: 21 Д: 23

Решение

Числа 1, 4, 10 и 13 можно разбить на пары 1+13=4+10. Числа из этих пар нужно будет записать в противоположные ячейки. Тогда суммы в строке и столбце будут равны 1+13+7=21.
Ответ: Г: 21

Задача К13 олимпиады по математике Кенгуру 2010

Уровень: Кадет (7 и 8 класс)

Условие

Кате нужно 18 минут, чтобы из трех коротких цепочек составить одну длинную. Для этого она использует дополнительные кольца. Сколько времени нужно девочке для того, чтобы составить цепочку из шести коротких?

Варианты ответа:

А: 27 мин Б: 30 мин В: 36 мин Г: 45 мин Д: 60 мин

Решение

Чтобы из трех коротких цепочек составить одну длинную, нужно выполнить два соединения. Значит на одно соединение Катя тратит 9 минут. Чтобы составить цепочку из шести коротких, нужно выполнить пять соединений, это займёт 45 минут.

Ответ: Г: 45 мин

Задача Ю12 олимпиады по математике Кенгуру 2010

Уровень: Юниор (9 и 10 класс)

Условие

Катя едет на каникулы в город Верону и планирует хоть раз пройти по каждому из пяти крупнейших мостов через реку Адидже. Девушка начинает свою прогулку от трамвайной остановки, к которой должна вернуться, пройдя по каждому из выбранных мостов и только по ним. Во время своей прогулки Катя перешла через реку n раз. Чему может равняться n?

Варианты ответа:

А: 3 Б: 4 В: 5 Г: 6 Д: 7

Решение

Т.к. мостов 5, и по каждому нужно пройти хотя бы раз, то . Но чтобы после n переходов через реку остаться на той же стороне, откуда началась прогулка, n должно быть чётным. Из вариантов ответа этим двум условиям удовлетворяет только число 6

Ответ: Г: 6

Задача В11 олимпиады по математике Кенгуру 2010

Уровень: Выпускник (11 класс)

Условие

Каким может быть количество ребер призмы?

Варианты ответа:

А: 100 Б: 200 В: 2008 Г: 2009 Д: 2010

Решение

Рассмотрим призму с n-угольником в основании. Тогда в нижнем основании будет n рёбер, ещё n рёбер – в верхнем, и ещё n рёбер будут соединять вершины нижнего и верхнего оснований. Всего 3n рёбер.

Значит, количество рёбер призмы должно делиться на 3. Из приведённых вариантов только число 2009 не делится на 3.

Ответ: Г: 2009

Задача Ю10 олимпиады по математике Кенгуру 2010

Уровень: Юниор (9 и 10 класс)

Условие



Пусть АВСЕ - квадрат, ВСР и СОЕ - равносторонние треугольники (см. рис). Если АВ = 1, то РО =

Варианты ответа:

А: Б: В: Г: Д:

Решение

Т.к. треугольники ВСР и СОЕ – равносторонние, то углы FCB и ECD равны по 60 градусов. Тогда . А .
Выходит, в равнобедренном треугольнике DCF угол при вершине – прямой. Значит

Ответ: А:

Задача К9 олимпиады по математике Кенгуру 2010

Уровень: Кадет  (7 и 8 класс)

Условие
Наименьшее двузначное число среди предложенных в ответах, которое нельзя представить в виде суммы трех различных однозначных чисел, равно:

Варианты ответа:
А: 10 Б: 15 В: 23 Г: 25 Д: 28

Решение

Имея три разных однозначных числа, можно получить сумму не более 9+8+7 = 24. Значит число 25 – наименьшее из вариантов, которые представить таким образом невозможно.


Ответ: Г: 25

Задача Ш8 олимпиады по математике Кенгуру 2010

Уровень: Школьник, Малыш 3-4  (3, 4, 5 и 6 класс)

Условие



На канате, который с обоих концов держат Андрей и Рома, завязан 21 узел. Ребята начинают считать узлы, двигаясь навстречу друг другу. Они встретились на узле, который Андрей насчитал десятым. Каким по счету был этот узел для Ромы?

Варианты ответа:

А: 15 Б: 14 В: 13 Г: 12 Д: 10

Решение

Первый узел для Андрея будет двадцать первым для Ромы. Второй узел для Андрея будет двадцатым узлом для Ромы и т.д. Замечаем закономерность: сумма номеров узлов для Андрея и для Ромы всегда равна 22. Значит 10й узел для Андрея будет 12м для Ромы.

Ответ: Г: 12

Задача М34-7 олимпиады по математике Кенгуру 2010

Уровень: Малыш 3-4, Малыш 2 (2, 3 и 4 класс)
Условие


В школьной столовой борщ отдельно стоит 2 гривны, картошка с мясом - 4 гривны, десерт - 3 гривны. «Специальное меню», в которое входит набор «борщ, картошка с мясом, десерт», стоит 7 гривен. Сколько Ты сможешь сэкономить, заказав «специальное меню» вместо трех отдельных блюд?
Варианты ответа:

А: ничего Б: 1 грн. В: 2 грн. Г: 3 грн. Д: 4 грн.

Решение

За борщ, картошку с мясом и десерт по отдельности пришлось бы заплатить 2+4+3 = 9 гривен. Вместе же мы получим их за 7 гривен. Экономия 9-7 = 2 гривны
Ответ: В: 2 грн.

Задача Ш3 олимпиады по математике Кенгуру 2010

Уровень: Школьник, Малыш-2 (2, 5 и 6 класс)
Условие
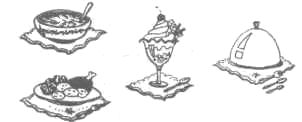
У мастера есть только плитки паркета с указанным слева рисунком. Какой из предложенных узоров невозможно создать, укладывая паркет в комнате?

Варианты ответа:


Решение

На плитка стрелка указывает из угла в угол. А в варианте Г на плитках стрелка указывает от стороны к стороне. Так что этот узор невозможен.
Ответ: Г

Задача М(3-4)5 олимпиады по математике Кенгуру 2010

Уровень: Малыш 3-4, Малыш 2 (2, 3 и 4 класс)

Условие
Вася и Володя пошли удить рыбу. Они вместе поймали на 7 рыб больше, чем Вася, и на 12 рыб больше, чем Володя. Сколько рыб поймали вместе Вася и Володя?

Варианты ответа:

А: 7 Б: 12 В: 15 Г: 19 Д: 22

Решение

Вася и Володя вместе поймали рыб больше одного Васи на столько, сколько рыб поймал Володя. Значит, Володя поймал 7 рыб. Аналогично рассуждая, находим, что Вася поймал 12 рыб. Всего они поймали 7+12=19 рыб.

Ответ: Г: 19

Задача Ш4 олимпиады по математике Кенгуру 2010

Уровень: Школьник (5 и 6 класс)

Условие

Урок длится 40 минут и начинается в 11:50. Ровно посредине урока в класс залетел воробей. В котором часу это произошло?

Варианты ответа:

А: 11:30 Б: 12:00 В: 12:10 Г: 12:20 Д: 12:30

Решение

Середина урока наступит через 20 минут после 11:50, т.е. в 12:10.

Ответ: В: 12:10

Уровень: Малыш 3-4 (3 и 4 класс)

Условие

Урок длится 40 минут, а начался в 11:50. В котором часу закончился урок?

Варианты ответа:

А: 11:90 Б: 12:10 В: 12:20 Г: 12:30 Д: 12:40

Решение

Через 40 минут после 11:50 наступит 12:30

Ответ: Г: 12:30

Задача К3 олимпиады по математике Кенгуру 2010

Уровень: Кадет (7 и 8 класс)

Условие

Игрушечные кенгуру упаковывают для отправки в магазин в коробки в форме куба. Каждые восемь коробок плотно упаковывают в большой картонный ящик, который также имеет форму куба. Сколько коробок с игрушками прилегают к дну большого ящика?

Варианты ответа:

А: 1 Б: 2 В: 3 Г: 4 Д: 8

Решение

Восемь коробок упакуются в куб 2х2х2, в слое, прилегающем к основанию, будет 2x2=4 коробки.

Ответ: Г: 4

Задача Ю2 олимпиады по математике Кенгуру 2010

Уровень: Юниор (9 и 10 класс)

Условие

Работая над тестом, Иван получил 85% баллов от максимально возможного результата. Тарас, имея тот же тест, получил на один балл больше, что составило 90% от максимально возможного результата. Какое наибольшее количество баллов можно было получить за этот тест?

Варианты ответа:

А: 5 Б: 17 В: 18 Г: 20 Д: 25

Решение

Разрыв в 1 балл равен разрыву в 5 процентов. Значит, 100 процентов составят 20 баллов.

Ответ: Г: 20

Задача В1 олимпиады по математике Кенгуру 2010

Уровень: Выпускник (11 класс)

Условие
График функции у = 5(х - 2)(х + 4) пересекает ось Ох в точках А и В. Найдите длину отрезка AB.

Варианты ответа:
А: 30 Б: 10 В: 6 Г: 5 Д: другой ответ

Решение

График будет пересекать ось Ох в корнях уравнения 5(х - 2)(х + 4) = 0. Это будут точки (-4; 0) и (2; 0). Расстояние между ними равно 6.

Ответ: В: 6